The limitation of GANs and VAE is that the generator of GANs or encoder of VAE must be differentiable. This prevents the model to generate a discrete output which can be useful for many tasks.
I start my study with Semi-supervised VAE [1]. This model is the same as CVAE but with an extra component for handling the unlabeled training dataset.
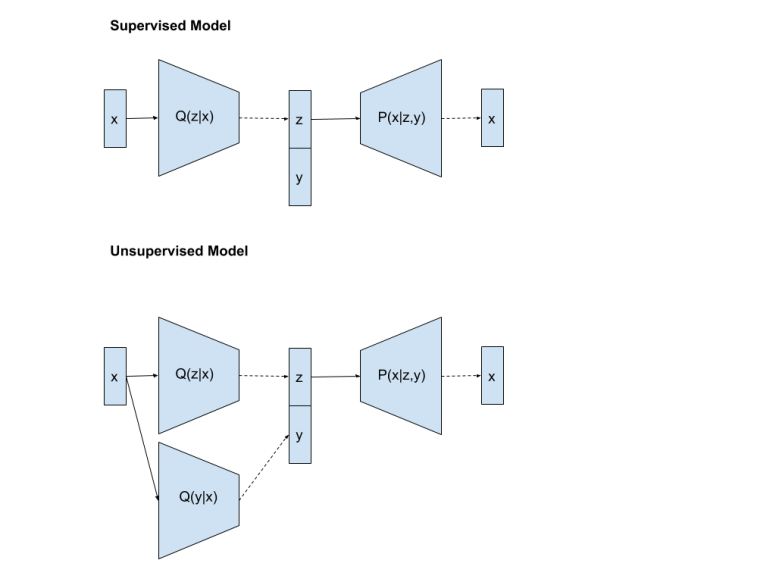
A semi-supervised model for VAE proposed by [1]
When the input has a label, we use the first architecture (which is CVAE) to train the model. When the input does not have a label, we use a discriminator to predict a label first. Then, we train the same way as labeled data.
To see the impact of unsupervised learning component, we can investigate the improvement of the generated images from the generator after adding unlabeled data.
First, we want to see how bad of the generated images after we train CVAE with the limited number of training samples:

Take 100% of images from each class (6000 images per class)

Take 10% of images from each class (600 images per class)

Take 1% of images from each class (60 images per class)

Take 0.1% of images from each class (6 images per class)
It is obvious that we don’t have enough data for VAE to approximate the image distribution.
Dealing with the Discrete output
It is quite straightforward to predict the label of the given unlabeled image first. But the real issue is that we cannot train CVAE end-to-end anymore because the output from the discriminator is a discrete output. We need to find the way to handle this situation.
Compute the Expectation directly (No Monte Carlo approximation)
The first approach to handle the discrete output from the encoder is to average out the reconstruction error for all possible discrete output. This is exactly what [1] did.
We factor  and derive the ELBO:
and derive the ELBO:
![E_{q(y|x)}[E_{q(z|x)}[\log P(x|z,y) - KL(q(z|x)||p(z))] - \log q(y|x)] =](https://s0.wp.com/latex.php?latex=E_%7Bq%28y%7Cx%29%7D%5BE_%7Bq%28z%7Cx%29%7D%5B%5Clog+P%28x%7Cz%2Cy%29+-+KL%28q%28z%7Cx%29%7C%7Cp%28z%29%29%5D+-+%5Clog+q%28y%7Cx%29%5D+%3D&bg=ffffff&fg=000&s=0&c=20201002)
![\sum_{y \in Y} q(y|x)[E_{q(z|x)}[\log P(x|z,y) - KL(q(z|x)||p(z))] - \log q(y|x)]](https://s0.wp.com/latex.php?latex=%5Csum_%7By+%5Cin+Y%7D+q%28y%7Cx%29%5BE_%7Bq%28z%7Cx%29%7D%5B%5Clog+P%28x%7Cz%2Cy%29+-+KL%28q%28z%7Cx%29%7C%7Cp%28z%29%29%5D+-+%5Clog+q%28y%7Cx%29%5D&bg=ffffff&fg=000&s=0&c=20201002)
Instead of sampling a label from  , [1] side-steped by expanding the expectation term. This approach is workable for the dataset with the small number of classes but it is not scalable when we have a lot of classes.
, [1] side-steped by expanding the expectation term. This approach is workable for the dataset with the small number of classes but it is not scalable when we have a lot of classes.
Reference:
[1] https://arxiv.org/abs/1406.5298

















You must be logged in to post a comment.